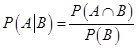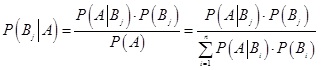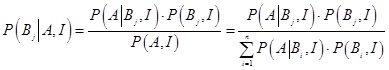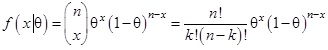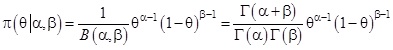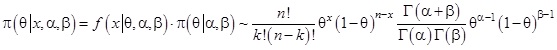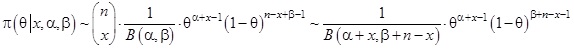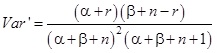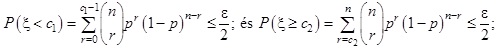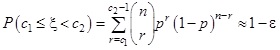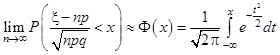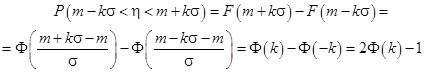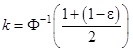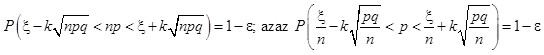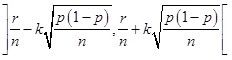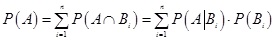
(2.1) képlet
Ha ezek után alkalmazzuk az  Boole-algebrai azonosságot és a feltételes valószínűség
Boole-algebrai azonosságot és a feltételes valószínűség 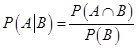 definícióját, akkor feltéve, hogy
definícióját, akkor feltéve, hogy 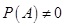 rögzített j indexre azt kapjuk, hogy
rögzített j indexre azt kapjuk, hogy
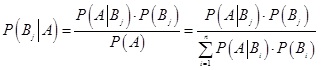
(2.2) képlet
Ez az összefüggés az eseményekre, illetve diszkrét eloszlásokra vonatkozó Bayes-tétel [2,3,4,5]. Itt szükséges megemlítenünk néhány elnevezést, amelyeket a továbbiakban használni fogunk:
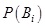 : „a priori” valószínűségek;
: „a priori” valószínűségek;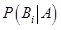 : „a posteriori” valószínűségek;
: „a posteriori” valószínűségek;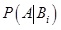 : „likelihood” valószínűségek.
: „likelihood” valószínűségek.
Az a priori jelző azt jelenti, hogy ezek a valószínűségek a kezdetben rendelkezésre álló információkat, a kezdeti tudásunkat tükrözik. Az elmélet lényegének hangsúlyozása szempontjából némileg kifejezőbb – bár kissé bonyolultabb – a tétel alakja, ha felhasználjuk, hogy az a priori valószínűségeket valamilyen I információ, input adatok, tudományos következtetés alapján kaptuk. Ekkor a következő összefüggésre jutunk:
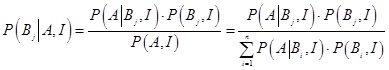
(2.3) képlet
Az alkalmazások bemutatása előtt szükséges hangsúlyoznunk néhány fontos tényt. Az a priori jelző azt jelenti, hogy az adott modellben úgy szerepelnek, mint kezdeti megfigyelés eredményei vagy mint a modell kezdeti elméleti paraméterei, amelyek származhatnak mérnöki, gazdasági, egyéb tudományos megfontolásokból. Az a posteriori valószínűségek a Bi események bekövetkezésének valószínűségét adják meg az A esemény, mint feltétel bekövetkezése mellett. Ezek voltaképpen az a priori valószínűségek frissítésének tekintendők. Éppen ebben áll az elmélet legfontosabb tulajdonsága: ha bekövetkezik egy esemény (adott esetben az A), akkor ennek ismeretében a kezdeti feltevéseink, amelyek, tekintettel a problémakör jellegére, meglehetősen csekély mennyiségű adat felhasználásával lettek megállapítva, módosíthatók, frissíthetők úgy, hogy tekintetbe vehetünk újabb adatokat, ebben az esetben az A esemény bekövetkezését. Fontos kiemelni, hogy az a priori valószínűségek diszkrét valószínűség eloszlást alkotnak, azaz teljesül, hogy 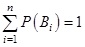 . Ugyanez igaz az a posteriori valószínűségekre is, vagyis:
. Ugyanez igaz az a posteriori valószínűségekre is, vagyis: 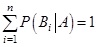 . A likelihood valószínűségek azok, amelyek az A esemény bekövetkezésének valószínűségét adják meg a Bi esemény, mint feltétel bekövetkezése mellett. Ezek a valószínűségek általában nem alkotnak eloszlást, tehát
. A likelihood valószínűségek azok, amelyek az A esemény bekövetkezésének valószínűségét adják meg a Bi esemény, mint feltétel bekövetkezése mellett. Ezek a valószínűségek általában nem alkotnak eloszlást, tehát 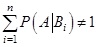 . A Bayes-tétel nevezőjében levő P(A) valószínűség „csak egy valós szám”, közvetlenül nem függ az a priori eloszlástól, matematikai szempontból egy normáló tényező, a szerepe lényegében az, hogy az a posteriori valószínűségek eloszlást alkossanak.
. A Bayes-tétel nevezőjében levő P(A) valószínűség „csak egy valós szám”, közvetlenül nem függ az a priori eloszlástól, matematikai szempontból egy normáló tényező, a szerepe lényegében az, hogy az a posteriori valószínűségek eloszlást alkossanak.
A Bayes-analízis feladata egyrészt az a priori és a likelihood valószínűségek becslése modellfeltevések, megfigyelések, tudományos következtetések alapján, majd pedig a Bayes-tétel felhasználásával a modellek frissítése a modellben szereplő paraméterek értékeinek módosításán keresztül [2,3,4,5].
A Bayes analízist a binomiális eloszlás p paraméterének pontbecslésére illetve a becslés javítására fogjuk alkalmazni. Vizsgáljunk tehát egy olyan modellt, amelyben a likelihood függvény binomiális eloszlással adott, ahol modellparaméterek az n és p. Nyilvánvaló a probléma természetéből adódóan, hogy a „kritikus” paraméter ebben az esetben a vizsgált esemény p valószínűsége. Mivel 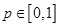 , ezért a q = p paraméter modellezésére a priori eloszlásként a Beta(a, b) béta eloszlást alkalmazzuk [2], amely éppen a [0, 1] intervallumon van értelmezve, paraméterei a > 0, b > 0.
, ezért a q = p paraméter modellezésére a priori eloszlásként a Beta(a, b) béta eloszlást alkalmazzuk [2], amely éppen a [0, 1] intervallumon van értelmezve, paraméterei a > 0, b > 0.
- A likelihood függvény most tehát binomiális eloszlással adott
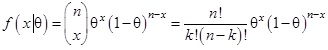
(2.4) képlet
az a priori eloszlás pedig béta eloszlással. Ez utóbbi a szokásos jelölésekkel
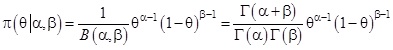
(2.5) képlet
ahol 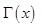 az analízisből ismert gamma függvény [2]. Mielőtt alkalmazzuk a Bayes-tételt, megadjuk a béta eloszlás jellemző adatait:
az analízisből ismert gamma függvény [2]. Mielőtt alkalmazzuk a Bayes-tételt, megadjuk a béta eloszlás jellemző adatait:
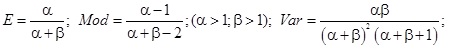
(2.6) képlet
ahol szokásosan E jelöli a várható értéket, Mod a móduszt, Var a szórásnégyzetet (variancia). Azért adtunk meg két jellemzőt is, mert bár a gyakorlatban a legtöbbször a várható értéket tekintjük pontbecslésként, ugyanolyan joggal használható adott esetben a módusz is.
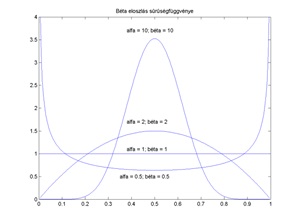
Az 1. ábrán a B(a, b) eloszlás sűrűségfüggvényét ábrázoltuk különböző a és b paraméterek esetén. Amit egyrészt hangsúlyozunk, az a = b eset, amikor B(a, a) sűrűségfüggvénye szimmetrikus az 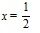 pontra, ez látható az 1. ábrán. Ha a = 1, akkor az egyenletes eloszlást kapjuk, ezt használhatjuk akkor, ha semmiféle kezdeti információnk nincs a p paraméter értékére. H a > 1 akkor a sűrűségfüggvénynek maximuma van az
pontra, ez látható az 1. ábrán. Ha a = 1, akkor az egyenletes eloszlást kapjuk, ezt használhatjuk akkor, ha semmiféle kezdeti információnk nincs a p paraméter értékére. H a > 1 akkor a sűrűségfüggvénynek maximuma van az 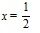 helyen, ha pedig a < 1, akkor ugyanezen a helyen minimum van.
helyen, ha pedig a < 1, akkor ugyanezen a helyen minimum van.
a) b)
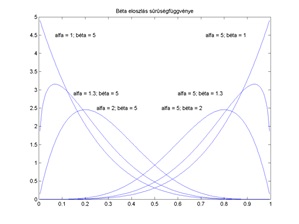
A Béta eloszlás sűrűségfüggvénye a) a = β; b) a ≠ β esetén (1. ábra)
Ha olyan információk birtokában vagyunk, amely szerint p értéke kicsi, közel van 0-hoz, illetve ellenkezőleg, ha p értéke nagy, közel van az 1-hez, akkor az 1. b) ábrán látható aszimmetrikus eloszlások közül választhatunk. A vizsgált problémakör, vagyis a biometrikus azonosító rendszerek esetében nyilvánvalóan igény, hogy a p valószínűség értéke kicsi legyen, ezért a témakör szempontjából elsősorban az 1. b) ábra kis p értékre vonatkozó görbéi az irányadók.
A gyakorlatban a következőt tesszük: ha arról van információnk, hogy a p paraméter értéke kicsi, akkor választunk egy olyan α és β paraméterpárt, amely az ábrán látható módon a kis p valószínűségre koncentrálódik, azaz aszimmetrikus és maximuma egy alkalmas kis p értéknél van. Ezután alkalmazzuk a (2.6) összefüggéseket, a p értékét a béta eloszlás várható értékével vagy móduszával modellezzük. Ez az a priori információ, amely csupán a modellfeltevésekből és a problémával kapcsolatos szubjektív ítéletünkből adódik. Ez valóban szubjektív ítélet, több szempontból is. Azonban éppen ez a Bayes-analízis páratlan előnye a matematika egyéb apparátusaival szemben. Arról van szó, hogy a szubjektivitást matematikai módszerekkel tekintetbe lehet venni. Az alábbiakból kiderül, hogy ez a szubjektivitás fokozatosan kiküszöbölődik a vizsgálataink során a becsült értékekből, ha elég sok megfigyelést végzünk. Ez más szóval azt jelenti, hogy ha rendelkezésünkre áll kellő számú adat, akkor a Bayes-analízis eszközeivel egyre objektívebb eredményt kapunk. Ennek a kifejtése következik az alábbiakban.
Alkalmazzuk tehát a Bayes-tételt, határozzuk meg az a posteriori eloszlást. Eltekintve a nevezőbeli normáló tényezőtől, a hiperparamétereket is hangsúlyozva, írhatjuk, hogy:
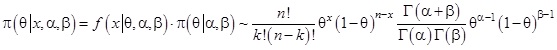
(2.7) képlet
Ha elvégezzük az összevonásokat, akkor eltekintve a konstans szorzóktól, a szokásos jelölésekkel az adódik, hogy
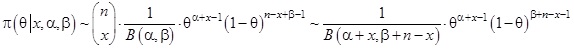
(2.8) képlet
A kapott a posteriori eloszlás ugyancsak béta eloszlás a + x, b + n – x paraméterekkel, tehát az a posteriori eloszlás: Beta(a + x, b + n – x). Az a posteriori eloszlásból kapjuk a binomiális eloszlás p paraméterének a frissített értékét. Erre alkalmazható elvileg a bemutatott paraméterek mindegyike, amelyeknek aktualizált értéke rendre:
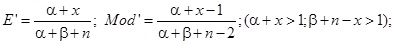
(2.9) képlet
A p paraméter értékét modellezzük tehát – a szokásos módon – a béta eloszlás várható értékével, amely kezdetben az 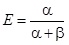 a priori becsléssel írható le. Ha ezek után végzünk n darab megfigyelést, és a megfigyelés eredménye az, hogy x = r alkalommal bekövetkezett a nemkívánatos esemény, és eszerint n – r alkalommal nem következett be, akkor a p valószínűség frissített értéke
a priori becsléssel írható le. Ha ezek után végzünk n darab megfigyelést, és a megfigyelés eredménye az, hogy x = r alkalommal bekövetkezett a nemkívánatos esemény, és eszerint n – r alkalommal nem következett be, akkor a p valószínűség frissített értéke 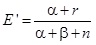 . Itt elvégezhetünk egy egyszerű elemzést az a priori és a posteriori eloszlások összehasonlítására. Vezessük be a
. Itt elvégezhetünk egy egyszerű elemzést az a priori és a posteriori eloszlások összehasonlítására. Vezessük be a 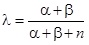 jelölést, amikor is
jelölést, amikor is 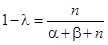 . Ekkor a p paraméter a posteriori eloszlás alapján aktualizált értéke felírható az
. Ekkor a p paraméter a posteriori eloszlás alapján aktualizált értéke felírható az 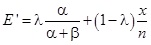 konvex lineáris kombináció alakjában, ahol az értelmezés szerint teljesül, hogy
konvex lineáris kombináció alakjában, ahol az értelmezés szerint teljesül, hogy 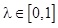 . Ahogyan l változik 0-tól 1-ig, E’ értéke változik
. Ahogyan l változik 0-tól 1-ig, E’ értéke változik 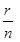 és E között.
és E között.
Következtetéseink az alábbiak:
Mérési adatok nélkül l = 1, tehát a modellparaméter éppen a béta eloszlás várható értéke, 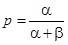 .
.
Ha növeljük a megfigyelések n számát, l értéke csökken, határesetben, ha n ® ∞ , akkor l ® 0. Ebben az esetben E’ ® 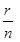 , ez pedig éppen a maximum likelihood becsléssel kapott érték. Ez azt jelenti, hogy ha sok a mérési adat, egyre kevéssé dominál a szubjektívnek tekinthető a priori béta eloszlás, egyre kisebb a hatása az a posteriori eloszlásra.
, ez pedig éppen a maximum likelihood becsléssel kapott érték. Ez azt jelenti, hogy ha sok a mérési adat, egyre kevéssé dominál a szubjektívnek tekinthető a priori béta eloszlás, egyre kisebb a hatása az a posteriori eloszlásra.
Ha n ® ∞, akkor tekintettel arra, hogy a szórásnégyzet (Var) nevezője az n magasabb fokú polinomja, mint a számláló,
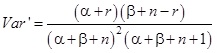
következik, hogy Var’ ® 0, tehát az a posteriori becslés bizonytalansága egyre kisebb.
A Bayes-analízis tehát a következőt teszi hozzá a ML-becsléssel kapott eredményhez. Tudjuk, hogy a legjobb pontbecslés a relatív gyakoriság. Ezt azonban csak akkor tudjuk érdemben használni, ha kellő számú megfigyelést végeztünk és ezen belül kellő számú alkalommal bekövetkezett a vizsgált esemény. Ha nincs elég adatunk, akkor szubjektív módon modellezzük a p valószínűséget. Ezt a szubjektív pontbecslő értéket tudjuk javítani a Bayes-analízis, közvetlenül a béta eloszlás alkalmazásával. Ezek szerint a pontbecslés annál jobb, minél több megfigyelést végzünk, ideálisan n → ∞ esetén kapunk pontos értéket.
Példa
Illusztráljuk a mondottakat egy példával.
- Tegyük fel, hogy a vizsgált rendszer egy bizonyos szempontból leírható binomiális eloszlással.
- Tegyük fel, hogy FRR-t kívánjuk modellezni.
- Kezdetben tegyük fel, hogy csak elméleti jóslataink vannak, de nincs mérési adatunk, még nem végeztünk megfigyelést.
- Az elméleti érték, vagyis az a priori becslés legyen FRR = 0,1.
- Ehhez alkalmazhatjuk a béta eloszlást, mint a priori becslést (2.6) szerint például az α = 1, β = 9 paraméterekkel.
- Tegyük fel, hogy végeztünk n = 100 megfigyelést, és ennek során bekövetkezett r = 9 téves elutasítás.
Ekkor (2.9) alapján azt mondhatjuk, hogy a FRR frissített, tehát a posteriori becslése
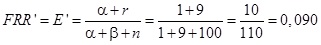
(2.10) képlet
a becsült érték tehát csökkent 9,0 százalékra.
- Tegyük fel, hogy újabb n = 150 megfigyelést végzünk, amelynek során a téves elutasítás bekövetkezik r = 5 alkalommal.
Ebben a lépésben a (2.10) becslést tekintjük a priori becslésnek, és ismét a (2.9) alapján frissítjük azt. Az a posteriori közelítés a második lépésben
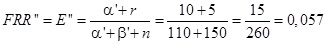
(2.11) képlet
FRR becsült értéke tehát a második lépésben ismét csökkent 5,7 százalékra (a monoton változás egyébként nem szükséges velejárója ennek az algoritmusnak). Az a priori becsléssel és a két a posteriori paraméterrel adott binomiális eloszlásokat szemléltetjük a 2. ábrán.
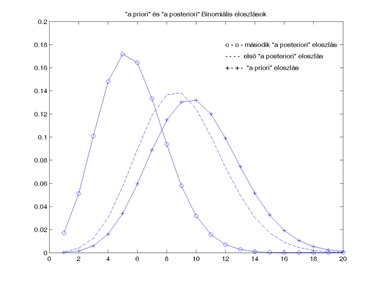
Az a priori és az a posteriori Binomiális eloszlások (2. ábra)
A mondottak szerint tehát abban biztosak lehetünk, hogy a megfigyelések számának növelésével a pontbecslés javul, de az is világos, hogy végtelen sok megfigyelést nem tudunk végezni, tehát a pontbecslésünk mindig tartalmaz majd bizonytalanságot. A következőkben azt vizsgáljuk meg, hogy mekkora ez a bizonytalanság, arra adunk útmutatást, hogy mennyi a „kellő számú megfigyelés” és mennyi a „vizsgált esemény kellő számú bekövetkezéseinek” a száma. A pontbecslésről ilyen módon áttérünk az intervallumbecslésre.
3. intervallumbecslés a binomiális eloszlás paraméterére vonatkozólag
A 2. pontban vizsgált pontbecslésnél többet mond, ha az ismeretlen p paraméter értékét egy intervallumba tudjuk elhelyezni adott valószínűséggel. Attól függően, hogy a kérdéses intervallum mekkora valószínűséggel tartalmazza a vizsgált paramétert, beszélhetünk különböző megbízhatósági szintű, úgynevezett konfidencia intervallumokról [5,6]. A konfidencia szintet általában 1 – ε jelöli, ahol ε > 0 egy alkalmasan választott kicsi pozitív szám. Ha az 1 – ε valós számot szorozzuk 100-zal, akkor százalékos formában kapjuk annak kifejezését, hogy az adott konfidencia intervallum milyen valószínűséggel tartalmazza a kérdéses p paramétert. A szokásos konfidencia szintek általában 90 százalék, 95 százalék és 99 százalék, amikor is az ε értéke rendre 0,1; 0,05 és 0,01. Az alábbi vizsgálatokban mi is ezeket a megbízhatósági szinteket vesszük alapul. A megbízhatósági intervallumok megszerkesztésének módja azon múlik, hogy hány megfigyelést tudtunk végezni, mekkora az n értéke. Ha az n egész szám kicsi, akkor közvetlenül a binomiális eloszlásra támaszkodva kapjuk ezeket, ha viszont az n értéke nagy, akkor a Moivre-Laplace tétel alapján a binomiális eloszlást közelíthetjük normális eloszlással. Ilyenkor közvetett módon hivatkozunk a binomiális eloszlásra, közvetlenül a normális eloszlást alkalmazzuk. Ezeket a kérdéseket fejtjük ki részletesen az alábbiakban.
1. eset: Az n értéke „kicsi”
Egyelőre nem tudunk konkrétumot mondani azzal kapcsolatban, hogy az n milyen esetben tekinthető „kicsi”-nek, erre visszatérünk a 2. eset vizsgálata során. Mindenesetre megjegyezzük, hogy az ebben az 1. esetben foglaltak tetszőleges n értékre pontosak. Ha az n egész szám meghalad egy bizonyos küszöbértéket – amely függ a p valószínűségtől –, a binomiális eloszlást közelíthetjük normális eloszlással. Nagy n-ek esetén a normális eloszlással való közelítés csak kényelmi szempont, egyszerűbb formulákat alkalmazhatunk, és kevesebb számítással érünk célhoz. Ha azonban n értéke kicsi, kénytelenek vagyunk az alábbiakban közölt formulákat alkalmazni.
Keresünk tehát egy olyan ]c1, c2[ intervallumot, amelyben a binomiális eloszlású ξ valószínűségi változó értéke 1 – ε valószínűséggel benne van. Tehát kétoldali konfidencia intervallumot szerkesztünk [5,6] (létezik egyoldali konfidencia intervallum is, de a vizsgálatok azt mutatják, hogy nem kapunk jobban használható eredményeket, sőt ellenkezőleg). Ez azt jelenti, hogy előírjuk, a c1 és c2 valós szám legyen olyan, hogy teljesüljenek a következő egyenlőtlenségek
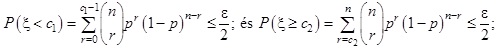
(3.1) képlet
vagyis keressük azt a ]c1, c2[ intervallumot, amelytől balra és jobbra a valószínűségi változó egyaránt 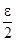 valószínűséggel vesz fel értéket, ahol c1 a maximális és c2 a minimális ilyen egész szám. Ekkor teljesül az a követelmény, hogy
valószínűséggel vesz fel értéket, ahol c1 a maximális és c2 a minimális ilyen egész szám. Ekkor teljesül az a követelmény, hogy
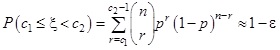
(3.2) képlet
tehát a ξ binomiális eloszlású valószínűségi változó értéke a ]c1, c2[ intervallumban van 1 – ε valószínűséggel. Ezek után a konfidencia intervallumok úgy adódnak, hogy adott n és ε esetén az r különböző értékeire meghatározzuk az (3.1) egyenleteknek eleget tevő c1 és c2 valós számokat, és ezeket ábrázoljuk koordináta rendszerben. Ilyen görbepárokat – tehát adott ε-hoz egy görbét a c1 és egy görbét a c2 egész számra – látunk a 3. ábrán ε = 0,01; 0,1 és 0,5 tehát rendre 99 százalék, 90 százalék és 50 százalék konfidenciaszint esetén.
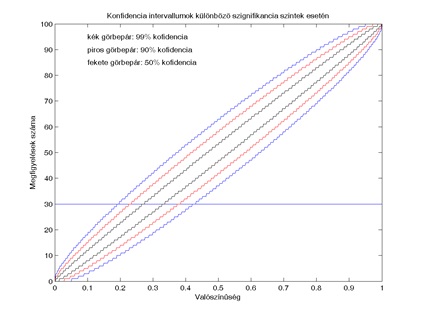
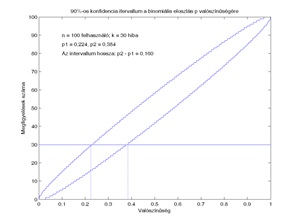
Konfidencia intervallumok maghatározása különböző megbízhatósági szintek és n = 100 megfigyelés esetén (3. ábra)
A konfidencia intervallumot úgy határozzuk meg, hogy figyelembe vesszük, hány alkalommal következett be a vizsgált esemény, azaz rögzítjük az r értékét. Ezek után az r ordinátánál illesztünk a koordináta rendszerben egy olyan egyenest, amely párhuzamos az abszcissza tengellyel. Ez az egyenes két pontban metszi a görbepárt. Ezen metszéspontok abszcisszái meghatározzák az 1 – ε szintű megbízhatósági intervallum két végpontját. Az ábrán az illusztráció kedvéért r = 30 estén illesztettünk egy egyenest. Amint az ábráról látszik, minél nagyobb konfidencia szintet írunk elő, rögzített r érték esetén, annál hosszabb intervallumot kapunk, amelybe 1 – ε valószínűséggel benne van a p valószínűség.
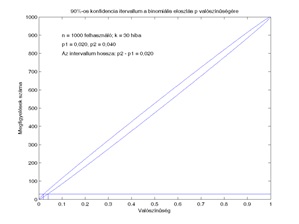
A 3. ábrán azonos n érték, tehát ugyanannyi megfigyelés esetén hasonlíthatjuk össze a megbízhatósági intervallumokat különböző konfidencia szintek esetén. A gyakorlat szempontjából azonban az is fontos, hogy hogyan módosulnak ezek a megbízhatósági intervallumok akkor, ha növelni tudjuk a megfigyelések n számát. A 4. a), b), c) és d) ábrákon az n értéke rendre 50, 100, 500 és 1000, de minden görbepár ugyanahhoz a 90 százalék megbízhatósági szinthez, tehát ε = 0,1 értékhez tartozik. Ebben az esetben az látható, hogy ha növeljük az n értékét, tehát a megfigyelések számát, akkor a konfidencia intervallumok szűkülnek. Minél több megfigyelést tudunk végezni, annál pontosabb kijelentést tudunk tenni a p paraméter értékére vonatkozólag. Azonban hangsúlyozunk egy fontos tényt, ami az ábrákra tekintve ugyancsak nyilvánvaló. A megbízhatósági intervallum nem kizárólag a megfigyelések számától, hanem a vizsgált esemény bekövetkeztéseinek r számától is függ. Ez az ábrákon úgy tükröződik, hogy ha más ordinátánál illesztünk a görbepárhoz egy egyenest, akkor a metszéspontok is máshova kerülnek, de ezek távolsága is függ a választott ordinátától.
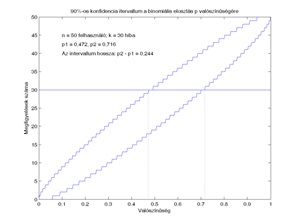
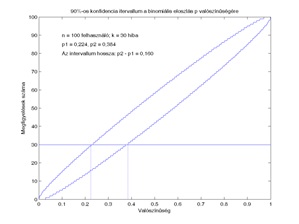
a) b)
c) d)
4. ábra
A binomiális eloszlás p paraméterére vonatkozó konfidencia intervallumok meghatározása különböző n értékek esetén.
A 3. és 4. ábrán szereplő nomogramok a következő módon használhatók a konfidencia intervallum meghatározására [5,6]. Kiválasztunk egy konkrét r értéket, azaz rögzítjük, hogy a vizsgált esemény az n megfigyelés során hány alkalommal következett be, majd meghatározzuk, hogy az azonosan r konstans függvény milyen abszcisszáknál metszi a görbepárokat . A konkrétum kedvéért mi az r = 30 értéket rögzítettük – ennek a későbbiekben szerepe lesz –, és erre vonatkozólag közlünk néhány adatot. A későbbi vizsgálatok érdekében nem csak az intervallumok végpontját, hanem a kapott intervallum hosszúságát is megadjuk.
|
n
|
p1
|
p2
|
intervallum hossza
|
|
50
|
0,472
|
0,716
|
0,244
|
|
100
|
0,224
|
0,384
|
0,160
|
|
500
|
0,042
|
0,080
|
0,038
|
|
1000
|
0,020
|
0,040
|
0,020
|
Konfidencia intervallumok a p paraméterre vonatkozólag különböző n értékek mellett (1. táblázat)
Amit ismét hangsúlyozni kívánunk, hogy a megbízhatósági intervallum két végpontja és annak hossza nem kizárólag a megfigyelések n számától függ, hanem attól is, hogy a megfigyelések során hány alkalommal regisztráltuk a megfigyelni kívánt eseményt.
Konkrétan ha az FRR vagy FAR értékekre vonatkozólag szeretnénk becslést adni, akkor nem elég a megfigyelések számát növelni, tehát a felhasználók n számát növelni vagy kellően nagynak választani a belépések számát, amikor a felhasználók szó szerint „használják” a rendszert, hanem az is szempont, hogy hány alkalommal regisztrálunk téves elutasítást vagy téves elfogadást. A cikksorozat 3. részében ezt a kérdést részletesen vizsgáljuk.
2. eset: Az n értéke „nagy”
Ebben az esetben megadjuk annak feltételét, hogy az n értékét mikor tekinthetjük kellően nagynak. A problémakör matematikai alapja a valószínűségelméletben Moivre-Laplace tétel néven ismert alapvető eredmény [2,3,4,5], amely szerint a binomiális eloszlás nagy n-ek esetén közelíthető normális eloszlással. Ez konkrétan azt jelenti, hogy ha n elég nagy, és az n és p paraméterekkel adott binomiális eloszlást standardizáljuk – tehát úgy transzformáljuk, hogy átlagértéke zérus, szórása pedig egység legyen –, akkor a standardizált binomiális eloszlás eloszlásfüggvénye a standard normális eloszlás eloszlásfüggvényével közelíthető, azaz
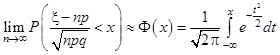
(3.3) képlet
Mivel a képletben szereplő integrandus nem integrálható, a Φ(x) függvény értékeit numerikus módszerekkel lehet meghatározni, így azokat táblázatból vehetjük [2]. Ezt a közelítést grafikusan szemléltetjük az ábrán olyan módon hogy a binomiális valószínűség eloszlást hasonlítjuk össze a megfelelő normális eloszlás sűrűségfüggvényével.
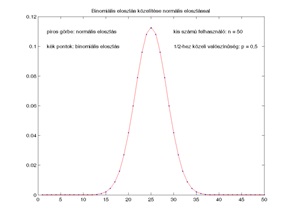
Az 5. a) ábrán az látható, hogy már viszonylag kis n esetén (n = 50) is jó az egyezés a két eloszlás között, ha a p értéke közel van 0,5-hez. Az 5. b) ábrán az látható, hogy a közelítés már nem olyan tökéletes, ha ugyanilyen kisszámú (n = 50) megfigyelés esetén a p értékét 0-hoz közeli kis számnak választjuk (az ábrán p = 0,1). Az 5. c) ábrán pedig az látható, hogyha kis p esetén növelni tudjuk a megfigyelések n számát, akkor az egyezés ugyancsak kielégítő lesz (az ábrán p = 0,1, n = 500). Azt természetesen a felhasználónak kell eldöntenie, hogy milyen pontosságot kíván meg a binomiális eloszlás normálissal való közelítése esetén. Azonban az a problémakör, amelyben a vázolt elméletet javasoljuk alkalmazni, világos, hogy kis p értékeket vizsgál (FRR, FAR, FIR értéke célszerűen alacsony), és ehhez relatíve nagyszámú megfigyelés szükséges a kielégítő pontosság elérése érdekében. Az 1. eset vizsgálata során felvetett „kis” n és „nagy” n kérdésének eldöntése attól függ, hogy milyen pontosságú a két eloszlás egyezése, ez azonban, mint láttuk az ábrán, függ a p-től is.
a)
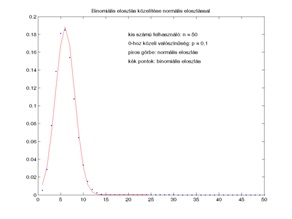
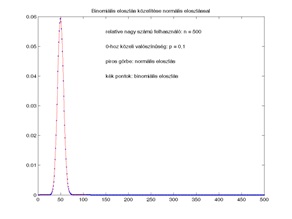
b) c)
Binomiális eloszlás közelítése normális eloszlással különböző n és p értékek esetén (5. ábra)
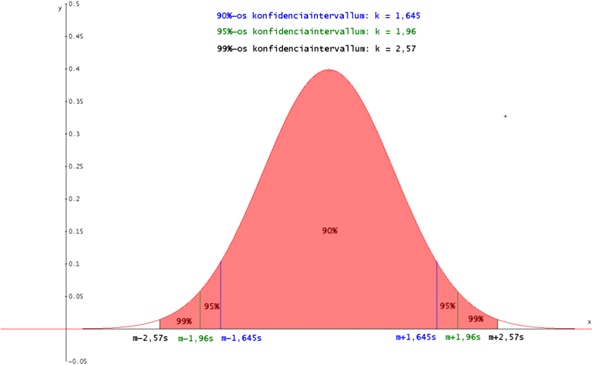
Maradva tehát az 1. esetben felvetett problémakör vizsgálatánál, a cél hogy konfidencia intervallumokat szerkesszünk a binomiális eloszlás normális eloszlással való közelítésének felhasználásával. A normális eloszlással kapcsolatban ismert és alapvető tény, hogy ha kijelölünk egy intervallumot az átlagértékre szimmetrikusan úgy, hogy a határok átlagtól való eltérése a szórás 1-, 2- illetve 3-szorosa, akkor a normális eloszlású valószínűségi változó értéke ezen intervallumokba rendre 68,26 százalék, 95,44 százalék, és 99,72 százalék eséllyel beleesik. Ezek az eredmények függetlenek attól, hogy a normális eloszlásnak mennyi az m átlagértéke és σ szórása. A megadott valószínűségek úgy adódnak, hogy alkalmazzuk a
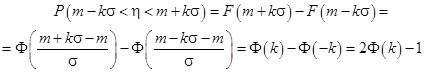
(3.4) képlet
összefüggést, ahol tehát k értéke a mondott esetekben rendre 1, 2 és 3, az F(x) függvény az N(m, σ) normális eloszlás eloszlásfüggvénye, Φ(x) függvény a standard normális eloszlás eloszlásfüggvénye [2,3,4,5], η pedig a normális eloszlású valószínűségi változót jelöli.
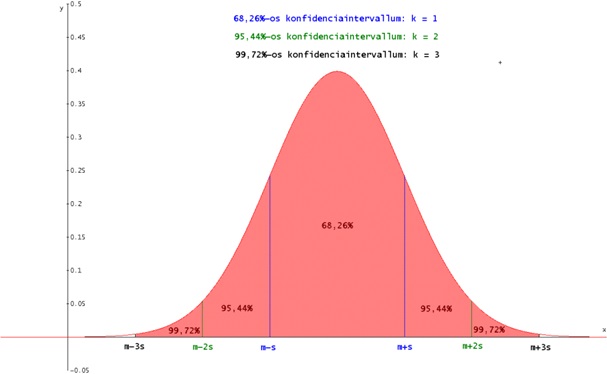
A normális eloszlás nevezetes konfidencia intervallumai (6. ábra)
A gyakorlatban azonban nem ezeket a – normális eloszlás szempontjából nevezetes – konfidencia szinteket alkalmazzuk, hanem ahogyan azt már említettük, a 90 százalék, 95 százalék és 99 százalék megbízhatósági szinteket.
A kérdést most feltesszük fordítva, kérdezzük tehát, hogy milyen k valós értékek tartoznak ezekhez a szokásos szintekhez. Ehhez az (3.4) egyenletet alkalmazzuk ismét.
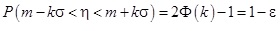
(3.5) képlet
ahonnan az eloszlásfüggvény invertálhatósága miatt adódik, hogy
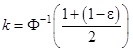
(3.6) képlet
Innen adott 1 – ε konfidencia szinthez táblázat alapján adódik a kérdéses k valós érték. Az általunk vizsgált és gyakorlatban szokásos 90 százalék, 95 százalék és 99 százalék esetekben a k értéke rendre 1,645; 1,96 és 2,57. Ezeket az intervallumokat szemlélteti a 7. ábra.
Ezek után a binomiális eloszlás p paraméterére vonatkozólag a következő módon kapjuk a megbízhatósági intervallumokat. Tegyük fel, hogy a normális eloszlású η valószínűségi változó az m várható értékére szimmetrikus intervallumba esik 1 – ε valószínűséggel. Ekkor tehát teljesül, hogy
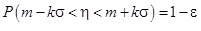
(3.7) képlet
az m várható értéket azonban nem ismerjük, hiszen ez a várható érték, ha a normális eloszlást a binomiális eloszlás közelítésére alkalmazzuk m = np amelyben p éppen az ismeretlen paraméter. Tehát közelítsünk az (3.7) képlethez fordított logikával. Az m értéke nem ismert de az η aktuális értéke igen, és (3.7) ekvivalens a
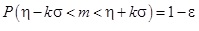
(3.8) képlet
amely szerint tehát 1 – ε a valószínűsége annak az eseménynek, hogy az ismeretlen m értéke beleesik egy olyan 2kσ hosszúságú intervallumba, amelynek középpontja az η aktuális – tehát változó – értéke. Ez a konfidencia intervallum igazi értelme. Az 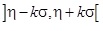 változó középpontú intervallum 1 – ε valószínűséggel tartalmazza az ismeretlen m várható értéket.
változó középpontú intervallum 1 – ε valószínűséggel tartalmazza az ismeretlen m várható értéket.
A hagyományos 90 százalék, 95 százalék és 99 százalék megbízhatósági szintekhez tartozó intervallumok meghatározása (7. ábra)
Ha a bevezetőben említett feltétel szerint a binomiális eloszlást kellő pontossággal közelíti a normális eloszlás, akkor az (3.8) összefüggést közvetlenül alkalmazhatjuk a binomiális eloszlású ξ valószínűségi változó m = np várható értékére és 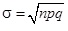 szórására, ahol alkalmazzuk a szokásos q = 1 – p egyszerűsítő jelölést.
szórására, ahol alkalmazzuk a szokásos q = 1 – p egyszerűsítő jelölést.
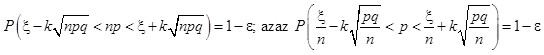
(3.9) képlet
Szerkesztettünk tehát egy könnyen számítható konfidencia intervallumot a binomiális eloszlás p paraméterére vonatkozólag. Ha tehát n megfigyelést végzünk és a megfigyelni kívánt esemény ξ = r alkalommal következik be, akkor az eloszlás p paramétere 1 – ε valószínűséggel benne van az
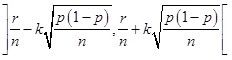
(3.10) képlet
intervallumban. Ha a szokásos 90 százalék, 95 százalék és 99 százalék megbízhatósági szinteket írjuk elő akkor (3.10) képletbe a k valós szám helyére rendre az 1,645; 1,96 és 2,57 értékek helyettesítendők. Lefordítva tehát a számítások eredményét közérthető nyelvre a következőt mondhatjuk. Ha végzünk n darab független megfigyelést és a vizsgált esemény r alkalommal bekövetkezik, akkor kiszámítjuk a vizsgált esemény 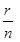 relatív gyakoriságát. Ez a p valószínűség legjobb pontbecslése, a ML-becslés. Azonban (3.10) alapján a p-re vonatkozólag ettől sokkal többet is állíthatunk, mégpedig azt, hogy a p tényleges – ám természetesen ismeretlen – értéke adott n és r egészek esetén 1 – ε valószínűséggel az (3.10) intervallumba esik. Láthatóan van egy kellemetlen vonása ennek az intervallumnak, az hogy a p paraméter értékét egy olyan intervallumba helyezi el adott valószínűséggel, melynek végpontjai függenek p-től. Ennek a problémának a kiküszöbölésével és a (3.10) megbízhatósági intervallum a részletes vizsgálatával foglalkozunk a következő cikkben.
relatív gyakoriságát. Ez a p valószínűség legjobb pontbecslése, a ML-becslés. Azonban (3.10) alapján a p-re vonatkozólag ettől sokkal többet is állíthatunk, mégpedig azt, hogy a p tényleges – ám természetesen ismeretlen – értéke adott n és r egészek esetén 1 – ε valószínűséggel az (3.10) intervallumba esik. Láthatóan van egy kellemetlen vonása ennek az intervallumnak, az hogy a p paraméter értékét egy olyan intervallumba helyezi el adott valószínűséggel, melynek végpontjai függenek p-től. Ennek a problémának a kiküszöbölésével és a (3.10) megbízhatósági intervallum a részletes vizsgálatával foglalkozunk a következő cikkben.
4. Összefoglalás
Cikksorozatunk 2. részében konkrét példán, a binomiális eloszlás vizsgálatán keresztül bemutattuk, hogyan lehet pontbecslést és intervallumbecslést alkalmazni bizonyos, eloszlást jellemző paraméterek értékének meghatározása, közelítése során. Ismét hangsúlyozzuk, hogy a módszerek általánosak, más eloszlások és más közvetlen alkalmazások esetén ugyanilyen logikával átgondolhatók. A következőkben, tehát a 3. részben azt mutatjuk majd be, hogyan használható a bemutatott elmélet konkrét biometrikus rendszer jellemzése, vizsgálata során.
Dr. Hanka László PhD., Óbudai Egyetem, Bánki Donát Gépész és Biztonságtechnikai Mérnöki Kar, Mechatronikai Intézet,
hanka.laszlo@bgk.uni-obuda.hu
Felhasznált irodalom
1. Hanka László: Matematikai módszerek a biometriában 1. A binomiális eloszlás alkalmazási lehetőségei ujjnyomat azonosító rendszerek vizsgálatában, a maximum likelihood elv alkalmazása
2. Denkinger Géza: Valószínűségszámítás. Tankönyvkiadó. Budapest. 1989. ISBN: 963 18 1552 8
3. William Feller: Bevezetés a valószínűségszámításba és alkalmazásaiba. Műszaki Könyvkiadó. Budapest. 1978. ISBN: 963 10 2070 3
4. Rényi Alfréd: Valószínűségszámítás. Tankönyvkiadó. Budapest, 1981. ISBN: 963175931 8
5. Prékopa András: Valószínűségelmélet műszaki alkalmazásokkal. Műszaki Könyvkiadó. Budapest. 1965
6. Bolla Marianna, Krámli András: Statisztikai következtetések elmélete. Typotex Kiadó Budapest, ISBN 9639548413
A sorozat cikkei
Matematikai módszerek a biometriában 1. A binomiális eloszlás alkalmazási lehetőségei ujjnyomat azonosító rendszerek vizsgálatában, a maximum likelihood elv alkalmazása
Matematikai módszerek a biometriában 2. A Bayes-analízis és az intervallumbecslés módszere ujjnyom azonosító rendszerek vizsgálatában
Matematikai módszerek a biometriában 3. A Doddington-féle 30-as szabályt és biometrikus rendszerek megbízhatóságának statisztikai elemzése
![]() , és összegük a biztos esemény, azaz
, és összegük a biztos esemény, azaz ![]() . Legyen továbbá A egy tetszőleges esemény. Ekkor a Teljes valószínűség tétele szerint [2,3,4,5] az A esemény bekövetkezésének valószínűsége a következő:
. Legyen továbbá A egy tetszőleges esemény. Ekkor a Teljes valószínűség tétele szerint [2,3,4,5] az A esemény bekövetkezésének valószínűsége a következő: